Capítulo 3 Análise de Componentes Principais

Felipe Micail da Silva Smolski

A técnica de Componentes Principais retoma informações de uma base de dados multivariada, transformando estes dados em variáveis de número igual ou inferior à amostra inicial e denominados “componentes principais”. Estes por sua vez, correspondem à combinação dos dados originais, sendo que representam uma redução de dimensionalidade dos dados originais em dois ou três componentes, identificando as direções pelas quais a variação dos dados são máximas, apresentando graficamente os resultados conforme Kassambara (2017 b). Ainda segundo este autor, são propósitos resumidos da anáise dae componentes principais:

Identificação de padrões ocultos dos dados;
Redução de dimensionalidade, pela diminuição da redundância nos dados;
Identificar variáveis correlacionadas.

3.1 Preparação dos dados

library(factoextra)

Carregando pacotes exigidos: ggplot2


Attaching package: 'ggplot2'

The following objects are masked from 'package:psych':

    %+%, alpha

Welcome! Related Books: `Practical Guide To Cluster Analysis in R` at https://goo.gl/13EFCZ


Attaching package: 'factoextra'

The following object is masked from 'package:agricolae':

    hcut

data("decathlon2", package = "factoextra")
head(decathlon2)

          X100m Long.jump Shot.put High.jump X400m X110m.hurdle Discus
SEBRLE    11.04      7.58    14.83      2.07 49.81        14.69  43.75
CLAY      10.76      7.40    14.26      1.86 49.37        14.05  50.72
BERNARD   11.02      7.23    14.25      1.92 48.93        14.99  40.87
YURKOV    11.34      7.09    15.19      2.10 50.42        15.31  46.26
ZSIVOCZKY 11.13      7.30    13.48      2.01 48.62        14.17  45.67
McMULLEN  10.83      7.31    13.76      2.13 49.91        14.38  44.41
          Pole.vault Javeline X1500m Rank Points Competition
SEBRLE          5.02    63.19  291.7    1   8217    Decastar
CLAY            4.92    60.15  301.5    2   8122    Decastar
BERNARD         5.32    62.77  280.1    4   8067    Decastar
YURKOV          4.72    63.44  276.4    5   8036    Decastar
ZSIVOCZKY       4.42    55.37  268.0    7   8004    Decastar
McMULLEN        4.42    56.37  285.1    8   7995    Decastar

decathlon2.active=decathlon2[1:23,1:10]

3.2 Criação dos componentes

library(FactoMineR)
pca=PCA(decathlon2.active, graph=TRUE)

pca

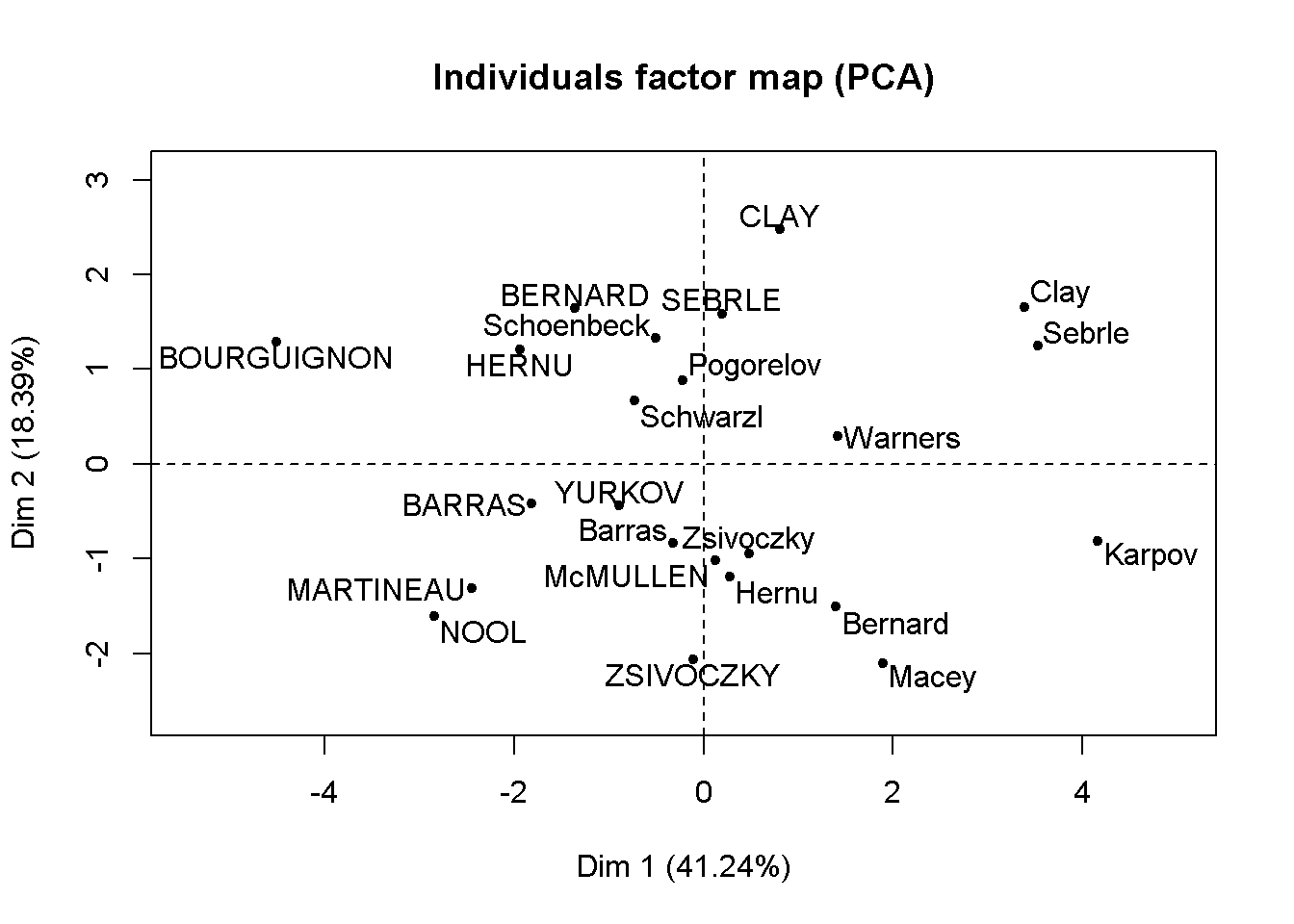
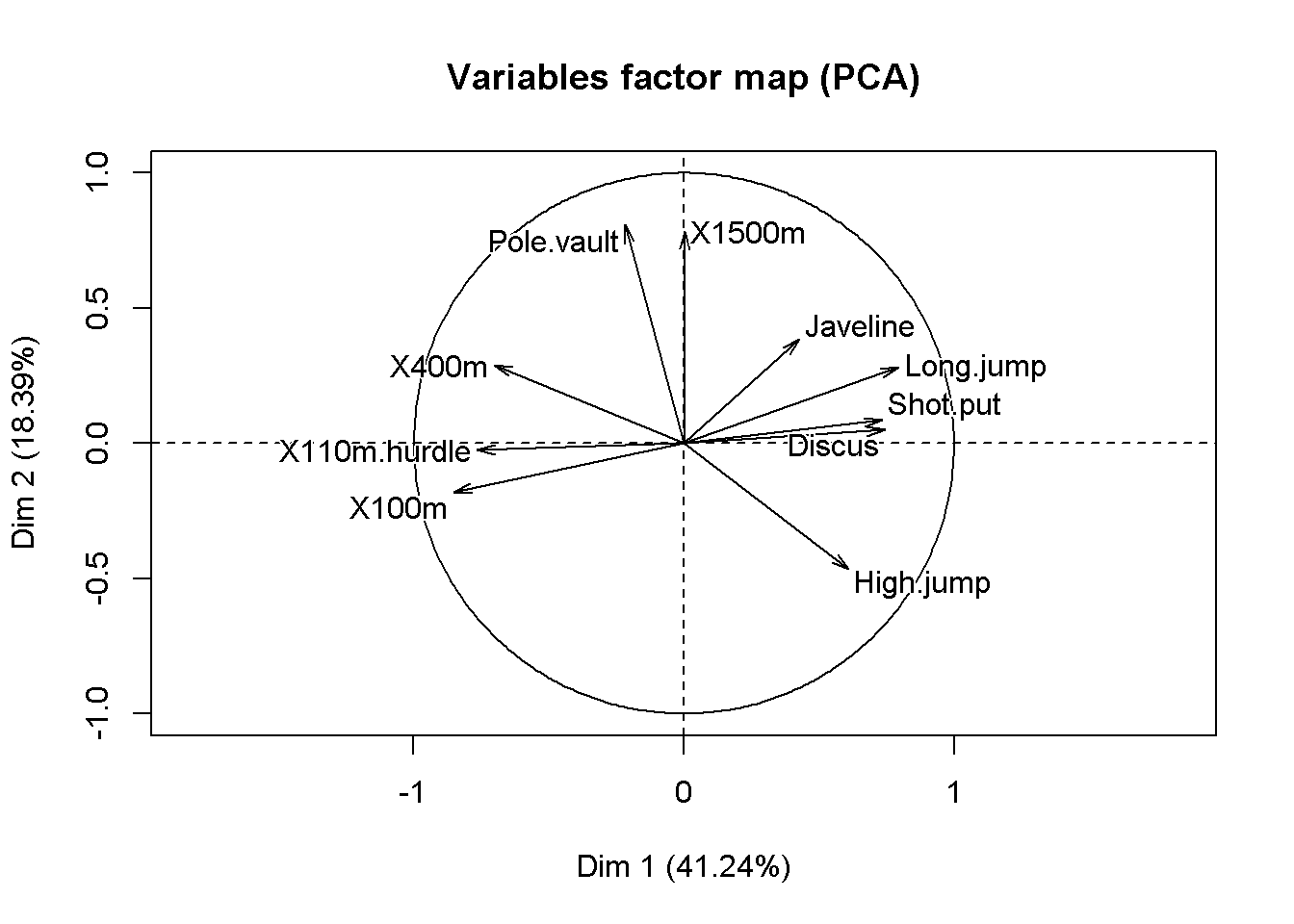
**Results for the Principal Component Analysis (PCA)**
The analysis was performed on 23 individuals, described by 10 variables
*The results are available in the following objects:

   name               description                          
1  "$eig"             "eigenvalues"                        
2  "$var"             "results for the variables"          
3  "$var$coord"       "coord. for the variables"           
4  "$var$cor"         "correlations variables - dimensions"
5  "$var$cos2"        "cos2 for the variables"             
6  "$var$contrib"     "contributions of the variables"     
7  "$ind"             "results for the individuals"        
8  "$ind$coord"       "coord. for the individuals"         
9  "$ind$cos2"        "cos2 for the individuals"           
10 "$ind$contrib"     "contributions of the individuals"   
11 "$call"            "summary statistics"                 
12 "$call$centre"     "mean of the variables"              
13 "$call$ecart.type" "standard error of the variables"    
14 "$call$row.w"      "weights for the individuals"        
15 "$call$col.w"      "weights for the variables"

A variância retida em cada um dos compomentes é medida pelos “autovalores” (eigenvalues), que podem ser extraídos utilizando a função get_eigenvalue():

library(factoextra)
autovalores=get_eigenvalue(pca)
autovalores

       eigenvalue variance.percent cumulative.variance.percent
Dim.1      4.1242           41.242                       41.24
Dim.2      1.8385           18.385                       59.63
Dim.3      1.2391           12.391                       72.02
Dim.4      0.8194            8.194                       80.21
Dim.5      0.7016            7.016                       87.23
Dim.6      0.4229            4.229                       91.46
Dim.7      0.3026            3.026                       94.48
Dim.8      0.2745            2.745                       97.23
Dim.9      0.1552            1.552                       98.78
Dim.10     0.1220            1.220                      100.00

Autovaloes superiores a 1 indicam que a variância do componente é superior ao que representaria a variância dos dados originais, sendo possível utilizar inclusive como ponto de corte para decidir quantos componentes utilizar. Observa-se que no exemplo acima, foram criados 10 componentes principais, dos quais os três primeiros explicam 72,02% da variação.

fviz_eig(pca, addlabels=TRUE, ylim = c(0,50))

variaveis=get_pca_var(pca)
head(variaveis$coord)

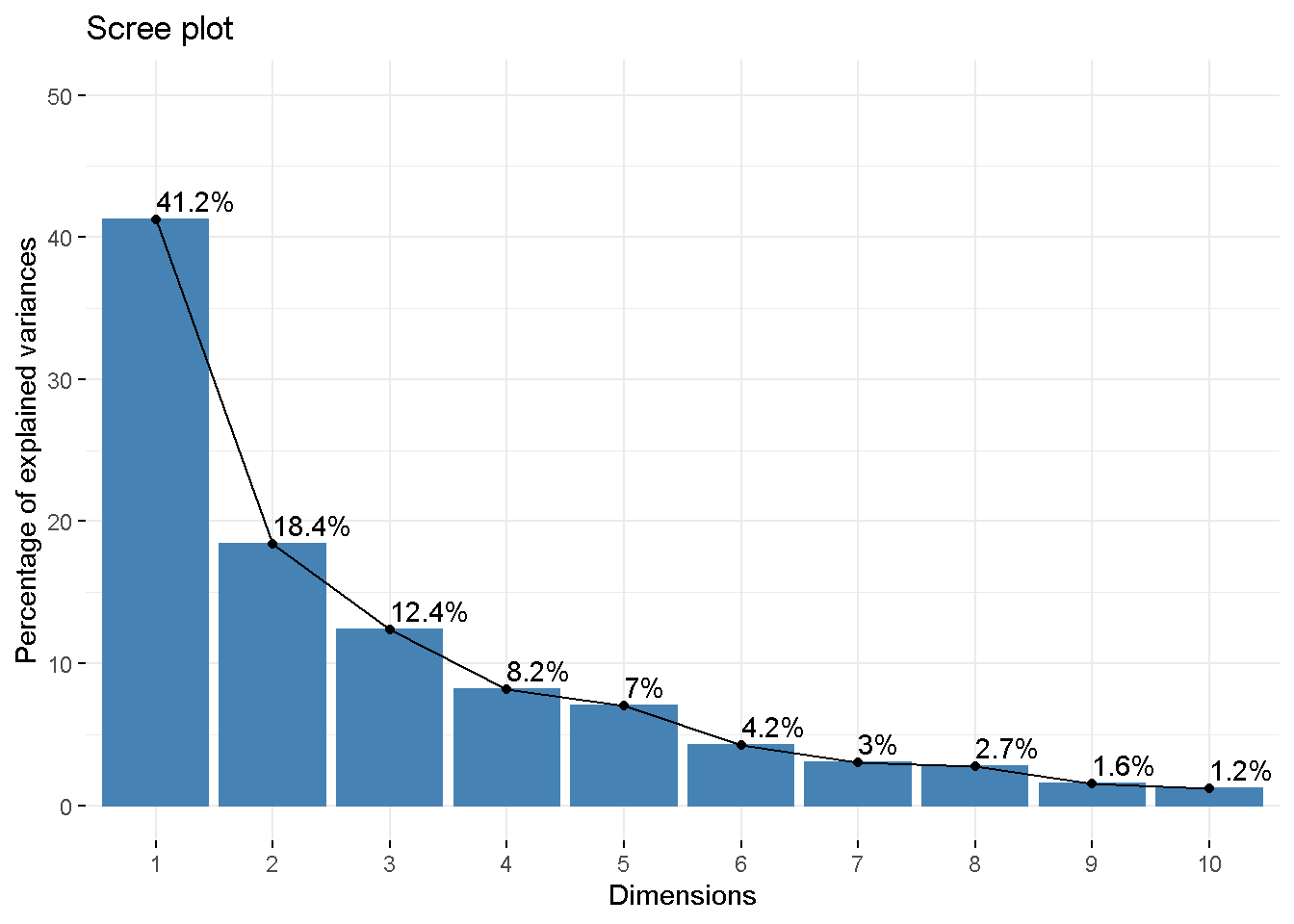
               Dim.1    Dim.2   Dim.3    Dim.4   Dim.5
X100m        -0.8506 -0.17940  0.3016  0.03357 -0.1944
Long.jump     0.7942  0.28086 -0.1905 -0.11539  0.2332
Shot.put      0.7339  0.08540  0.5176  0.12847 -0.2488
High.jump     0.6101 -0.46521  0.3301  0.14455  0.4027
X400m        -0.7016  0.29018  0.2835  0.43083  0.1039
X110m.hurdle -0.7641 -0.02474  0.4489 -0.01690  0.2242

Referências

Kassambara, Alboukadel. 2017b. Practical Guide To Principal Component Methods in R. 1 ed. USA: STHDA.