Capítulo 1 Delineamentos Experimentais

Tatiane Chassot

A experimentação é uma parte da estatística probabilística que estuda o planejamento, execução, coleta de dados, análise de dados e interpretação dos resultados provenientes de um experimento.

Um experimento é um procedimento planejado com base em uma hipótese, que tem por objetivo provocar fenômenos (tratamentos) de forma controlada, analisando e interpretando os resultados obtidos.

O tratamento é o método, elemento ou material cujo efeito desejamos avaliar em um experimento. Por exemplo: formas de preparo de solo, diferentes cultivares, doses de adubação, controle de insetos e outras pragas, controle de uma doença. Num experimento, somente o tratamento variade uma unidade experimental para outra, as demais condições são mantidas constantes, salvo erros não controláveis.

E alguns experimentos, utiliza-se a testemunha (nas ciências agrárias e ambientais) ou placebo (na saúde), que são as unidades experimentais que não recebem tratamento.

A unidade experimental é a unidade que recebe o tratamento uma vez e, normalmente são chamadas de parcelas. A escolha da unidade experimental depende dos tipos de tratamentos que serão avaliados. Podem ser: uma área de campo, um vaso com solo, um animal, uma placa de Petri, uma planta. Em áreas de campo, normalmente utiliza-se a bordadura. Num experimento, recomenda-se, no mínimo, a utilização de 20 UEs.

Em um experimento, a variável a ser avaliada chamamos de variável resposta. Por exemplo, número de grãos por planta, número de folhas por planta, altura das plantas.

1.1 Princípios básicos da Experimentação

1.1.1 Repetição

A repetição consiste na aplicação do mesmo tratamento sobre duas ou mais unidades experimentais. Permite estimar o erro experimental e avaliar de forma mais precisa o efeito de cada tratamento.

O erro experimental é caracterizado pela variância entre as unidades experimentais que receberam o mesmo tratamento.

1.1.2 Casualização

A casualização consiste na aplicação dos tratamentos aleatoriamente (sorteio) sobre as unidades experimentais. A casualização é usada para obter a independência dos erros, ou seja, evitar que determinados tratamentos sejam favorecidos.

1.1.3 Controle local

Quando tiver heterogeneidade no material experimental: plantas de diferentes alturas, animais de diferentes idades, solo com declividade, deve-se separar o material em grupos homogêneos e aplicar o tratamento uma vez dentro de cada grupo (blocos). A homogeneidade ou não do material dá origem aos tipos de delineamentos:

Delineamento Inteiramente Casualizado (DIC): material experimental homogêneo;
Delineamento Blocos Casualizados (DBC): material experimental com uma fonte de heterogeneidade;
Delineamento Quadrado Latino (DQL): material experimental com duas fontes de heterogeneidade.

1.2 Análise de Variância

Para saber se existe diferença significativa entre as médias resultados dos efeitos de tratamentos, realiza-se a Análise de Variância (ANOVA).

Nome da Tabela
Fonte de Variação	Graus de Liberdade (GL)	Soma de Quadrados (SQ)	Quadrado Médio (QM)	Falc	P
Tratamento	I-1	SQtrat	QMat	QMatr/QMerro	P
Erro	GLerro	SQerro	QMerro
Total	IJ-1	SQtotal

1.3 Hipóteses estatísticas

H\(_0\): Não existe diferença entre as médias dos tratamentos
H\(_1\): Existe, pelo menos, uma diferença entre as médias dos tratamentos

1.4 Delineamento Inteiramente Causalizado (DIC)

É utilizado quando as unidades experimentais são homogêneas. É o mais simples dos delineamentos e os tratamentos são designados às unidades experimentais de forma casualizada, por meio de um único sorteio. Usado principalmente em pequenos animais, casas de vegetação e em laboratórios.

Exemplo: Um produtor deseja avaliar 4 variedades de pera (A, B, C e D). Para tanto, instalou um experimento no delineamento inteiramente casualizado, utilizando 5 repetições por variedade. Os resultados, peso médio do fruto, estão apresentados a seguir:

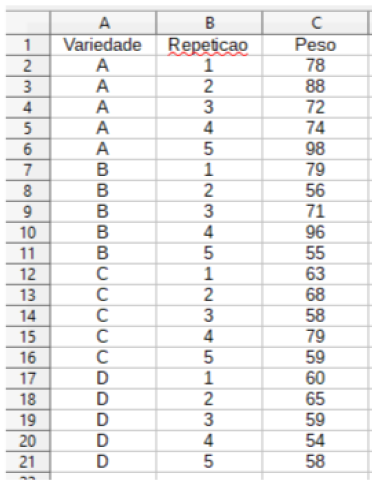
Figura 1.1: Variedades de pera separadas por grupos em faixas de peso e repetição

Existe diferença significativa entre as variedades de pera, considerando o peso médio dos frutos de cada variedade?

Para responder esta pergunta, utilizamos a Análise de Variância (ANOVA).

No software RStudio:

Criar o arquivo acima em planilha eletrônica. Nomear como DIC e salvar em formato .xls.

Importar no RStudio:

library(readxl)
url <- "https://github.com/Smolski/livroavancado/raw/master/dic.xls"
destfile <- "dic.xls"
curl::curl_download(url, destfile)
DIC <- read_excel(destfile)
attach(DIC)

O comando que gera a análise de variância é o aov() e o comando que exibe o quadro da ANOVA é o anova. Então, podemos gerar o quadro da análise de uma são vez associando os dois comandos.

anova=aov(Peso~Variedade)
summary(anova)

            Df Sum Sq Mean Sq F value Pr(>F)  
Variedade    3   1414     471    3.78  0.032 *
Residuals   16   1997     125                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Hipóteses estatísticas:

H\(_0\): ti \(=\) 0 (as médias dos tratamentos nãao diferem entre si)
H\(_1\): ti \(\neq\) 0 (existe, no mínimo, uma diferença entre as médias dos tratamentos)

Como p = 0,0319 (0,01 \(\leq\) p “menor ou igual a” 0,05), rejeita-se H\(_0\) com nível de significância de 5% e conclui-se que existe diferença significativa entre as médias dos tratamentos.

Para saber quais as médias que diferem, utilizamos o teste de Tukey.

attach(DIC)

The following objects are masked from DIC (pos = 3):

    Peso, Repeticao, Variedade

TukeyHSD(anova,as.factor("Variedade"),ordered=TRUE)

  Tukey multiple comparisons of means
    95% family-wise confidence level
    factor levels have been ordered

Fit: aov(formula = Peso ~ Variedade)

$Variedade
    diff     lwr   upr  p adj
C-D  6.2 -14.016 26.42 0.8164
B-D 12.2  -8.016 32.42 0.3429
A-D 22.8   2.584 43.02 0.0245
B-C  6.0 -14.216 26.22 0.8303
A-C 16.6  -3.616 36.82 0.1282
A-B 10.6  -9.616 30.82 0.4602

Para que o RStudio apresente uma tabela com as médias e letras indicando quais as médias que diferiram, devemos instalar o pacote agricolae.

library(agricolae)
library(gtools)
HSD.test(anova,as.factor("Variedade"),console=TRUE)


Study: anova ~ as.factor("Variedade")

HSD Test for Peso 

Mean Square Error:  124.8 

Variedade,  means

  Peso    std r Min Max
A 82.0 10.863 5  72  98
B 71.4 17.097 5  55  96
C 65.4  8.562 5  58  79
D 59.2  3.962 5  54  65

Alpha: 0.05 ; DF Error: 16 
Critical Value of Studentized Range: 4.046 

Minimun Significant Difference: 20.22 

Treatments with the same letter are not significantly different.

  Peso groups
A 82.0      a
B 71.4     ab
C 65.4     ab
D 59.2      b

*Médias dos tratamentos não seguidas por mesma letra diferem pelo teste de Tukey, ao nível de 5% de significância.

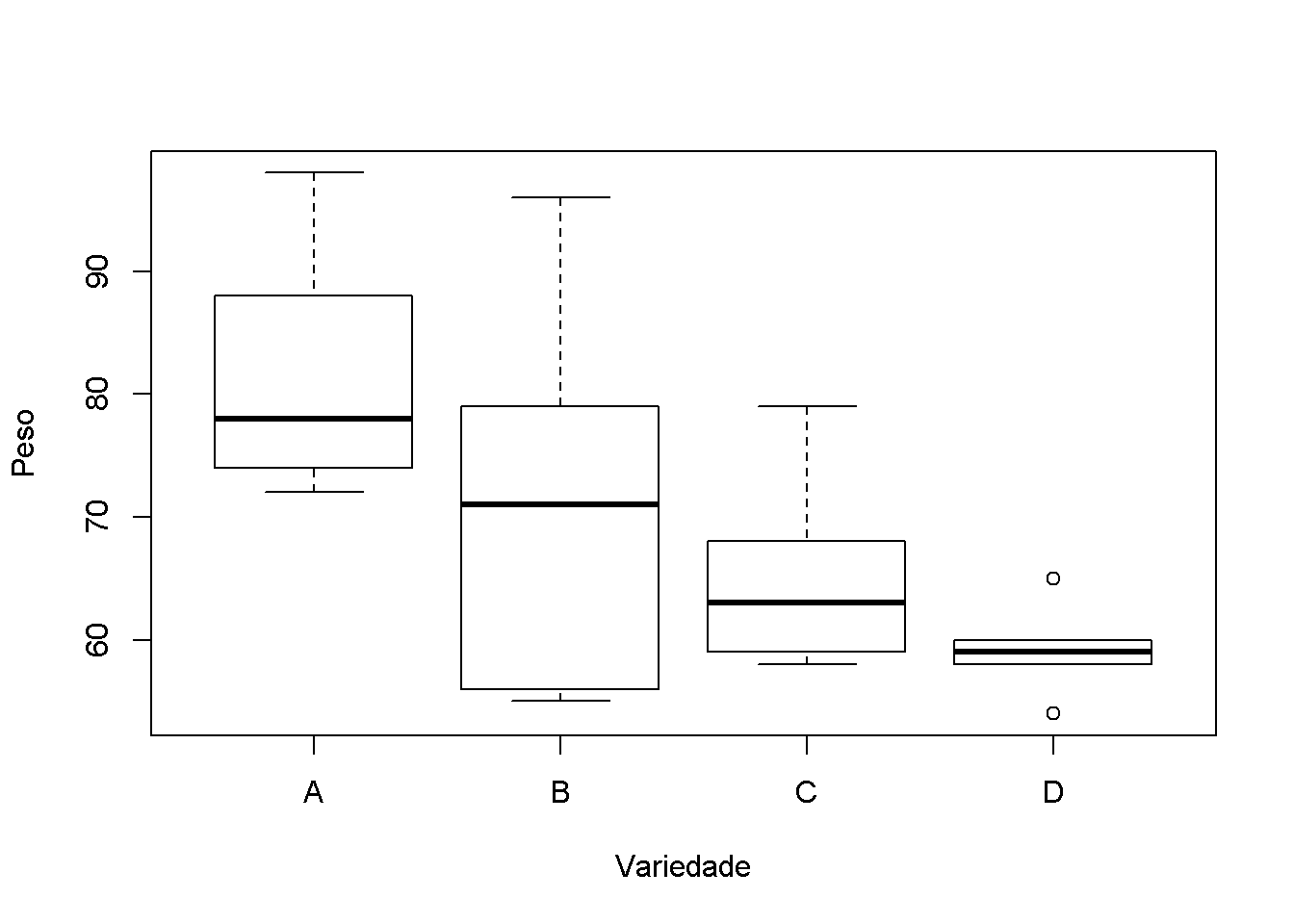
Conclusão: A variedade de pera A apresentou o maior peso médio dos frutos, que não diferiu significativamente do peso médio das variedades B e C. A variedade de pera D apresentou o menor peso médio dos frutos, que não diferiu significativamente do peso médio das variedades B e C. As variedades B e C apresentaram peso médio dos frutos intermediário.

attach(DIC)

The following objects are masked from DIC (pos = 5):

    Peso, Repeticao, Variedade

The following objects are masked from DIC (pos = 6):

    Peso, Repeticao, Variedade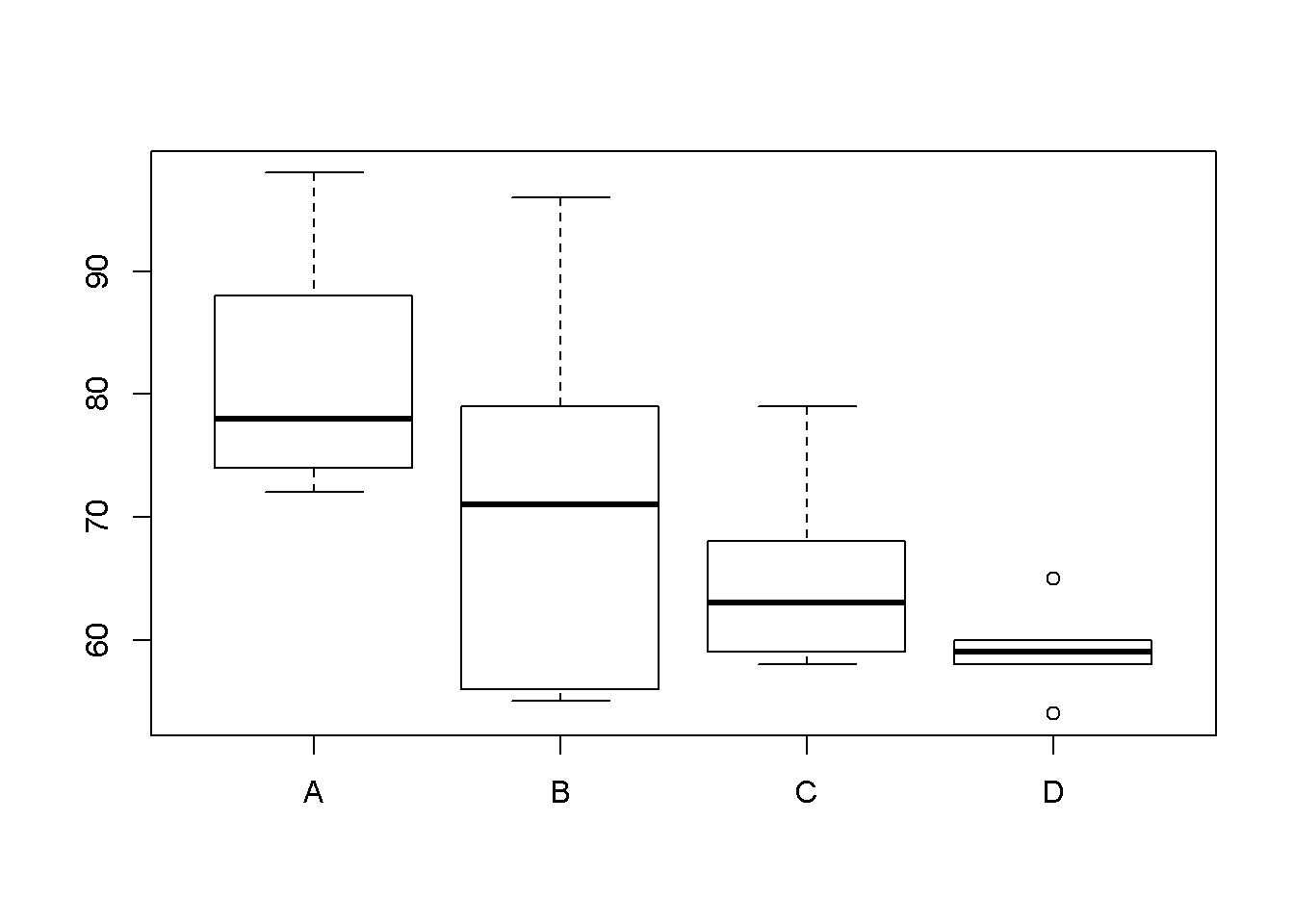

boxplot(Peso~Variedade)

boxplot(Peso~Variedade,xlab="Variedade",ylab="Peso")

tapply(Peso,Variedade,mean)

   A    B    C    D 
82.0 71.4 65.4 59.2

tapply(Peso,Variedade,sd)

     A      B      C      D 
10.863 17.097  8.562  3.962

residuos=residuals(anova)
ajustados=fitted(anova)
plot(ajustados,residuos)
abline(h=0)

qqnorm(residuos)
qqline(residuos)

1.5 Delineamento Blocos Casualizados (DBC)

É utilizado quando as unidades experimentais são heterogêneas. Os tratamentos são designados às unidades experimentais de forma casualizada, por meio de sorteio por blocos. Na área agrícola, é usado principalmente em áreas de campo e grandes animais.

Exemplo: Uma Nutricionista elaborou 4 dietas e quer aplicá-las em 20 pessoas a fim detestar suas eficiências quanto à perda de peso. Porém ela notou que entre essas 20 pessoas existem 5 grupos de faixas iniciais de peso. Então, para aumentar a eficácia do teste ela separou os 20 indivíduos em 5 grupos de faixas de peso.

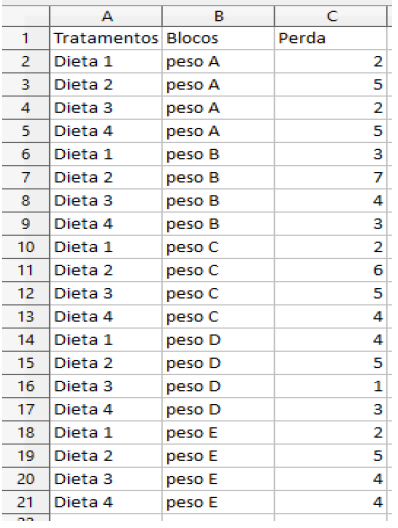
Figura 1.2: Indivíduos separados por grupos em faixas de peso

Criar o arquivo acima em planilha eletrônica. Nomear como DBC e salvar em formato .xls.

Importar no RStudio:

require(readxl)
url <- "https://github.com/Smolski/livroavancado/raw/master/dbc.xls"
destfile <- "dbc.xls"
curl::curl_download(url, destfile)
DBC  <- read_excel(destfile)

attach(DBC)
anova=aov(Perda~Tratamentos+Blocos)
summary(anova)

            Df Sum Sq Mean Sq F value Pr(>F)   
Tratamentos  3   25.2     8.4    6.00 0.0097 **
Blocos       4    3.2     0.8    0.57 0.6885   
Residuals   12   16.8     1.4                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Hipóteses estatísticas:

H\(_0\): ti \(=\) 0 (as médias dos tratamentos não diferem entre si)
H\(_1\): ti \(\neq\) 0 (existe, no mínimo, uma diferença entre as médias dos tratamentos)

Como p = 0,00973 (p \(\leq\) 0,01), rejeita-se H\(_0\) com nível de significância de 1% e conclui-se que existe diferença significativa entre as médias dos tratamentos.

H\(_0\): \(\sigma\)² blocos \(=\) 0
H\(_1\): \(\sigma\)² blocos \(\leq\) 0

Como p \(=\) 0,68854 (p \(\leq\) 0,05), não rejeita-se H\(_0\) e conclui-se que a variância entre os blocos não é significativa.

attach(DBC)
HSD.test(anova,as.factor("Tratamentos"),console=TRUE)


Study: anova ~ as.factor("Tratamentos")

HSD Test for Perda 

Mean Square Error:  1.4 

Tratamentos,  means

        Perda    std r Min Max
Dieta 1   2.6 0.8944 5   2   4
Dieta 2   5.6 0.8944 5   5   7
Dieta 3   3.2 1.6432 5   1   5
Dieta 4   3.8 0.8367 5   3   5

Alpha: 0.05 ; DF Error: 12 
Critical Value of Studentized Range: 4.199 

Minimun Significant Difference: 2.222 

Treatments with the same letter are not significantly different.

        Perda groups
Dieta 2   5.6      a
Dieta 4   3.8     ab
Dieta 3   3.2      b
Dieta 1   2.6      b

Médias dos tratamentos não seguidas por mesma letra diferem pelo teste de Tukey, ao nível de 5% de significância.

Conclusão: A dieta que resultou na maior perda de peso foi a dieta 2, que não diferiu da dieta 4. A dieta que resultou na menor perda de peso foi a dieta 1, que não diferiu das dietas 3 e 4.

Medidas descritivas com a variável resposta:

boxplot(Perda~Tratamentos)

boxplot(Perda~Tratamentos,xlab="Tratamentos",ylab="Perda")

tapply(Perda,Tratamentos,mean)

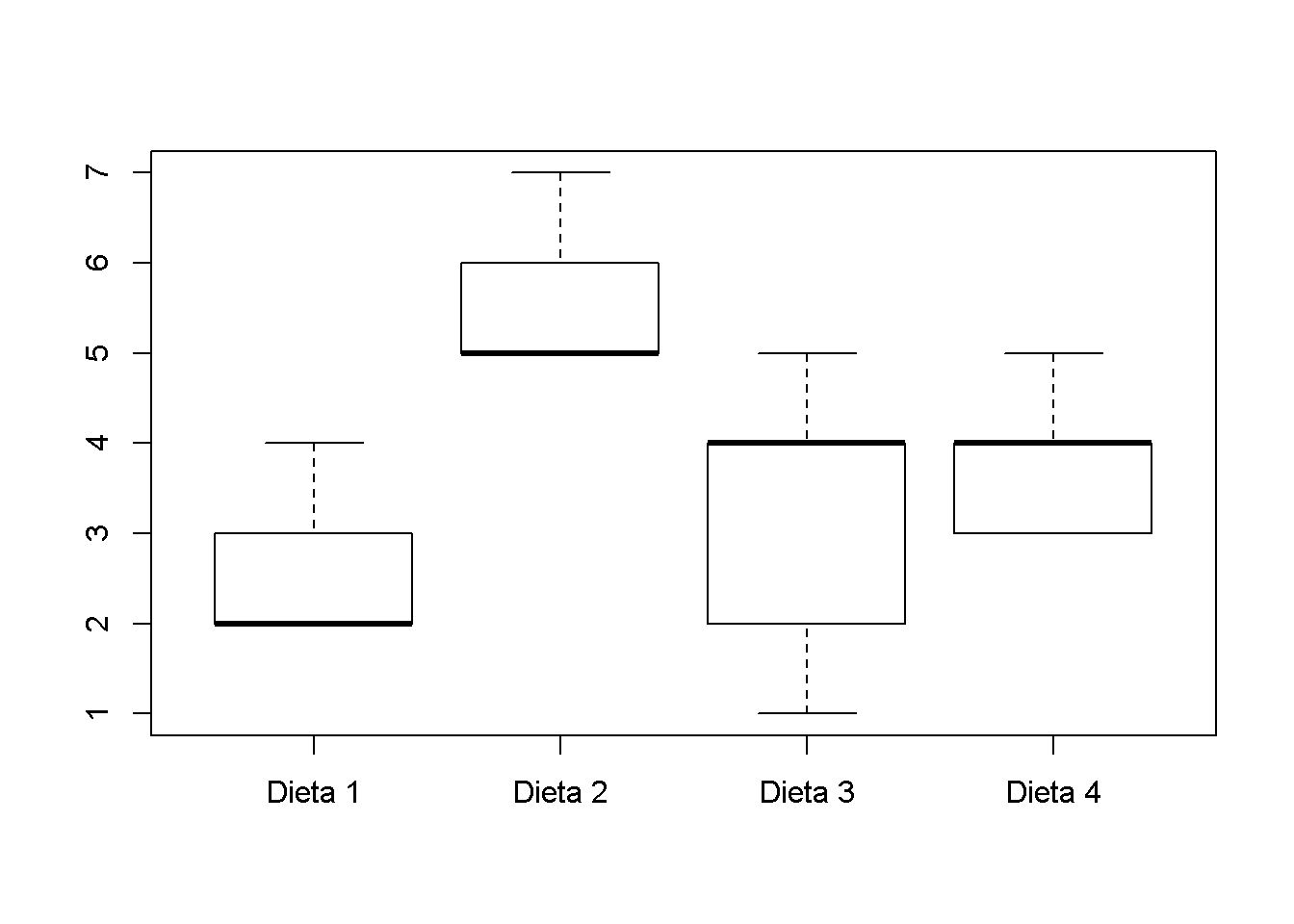
Dieta 1 Dieta 2 Dieta 3 Dieta 4 
    2.6     5.6     3.2     3.8

tapply(Perda,Tratamentos,sd)

Dieta 1 Dieta 2 Dieta 3 Dieta 4 
 0.8944  0.8944  1.6432  0.8367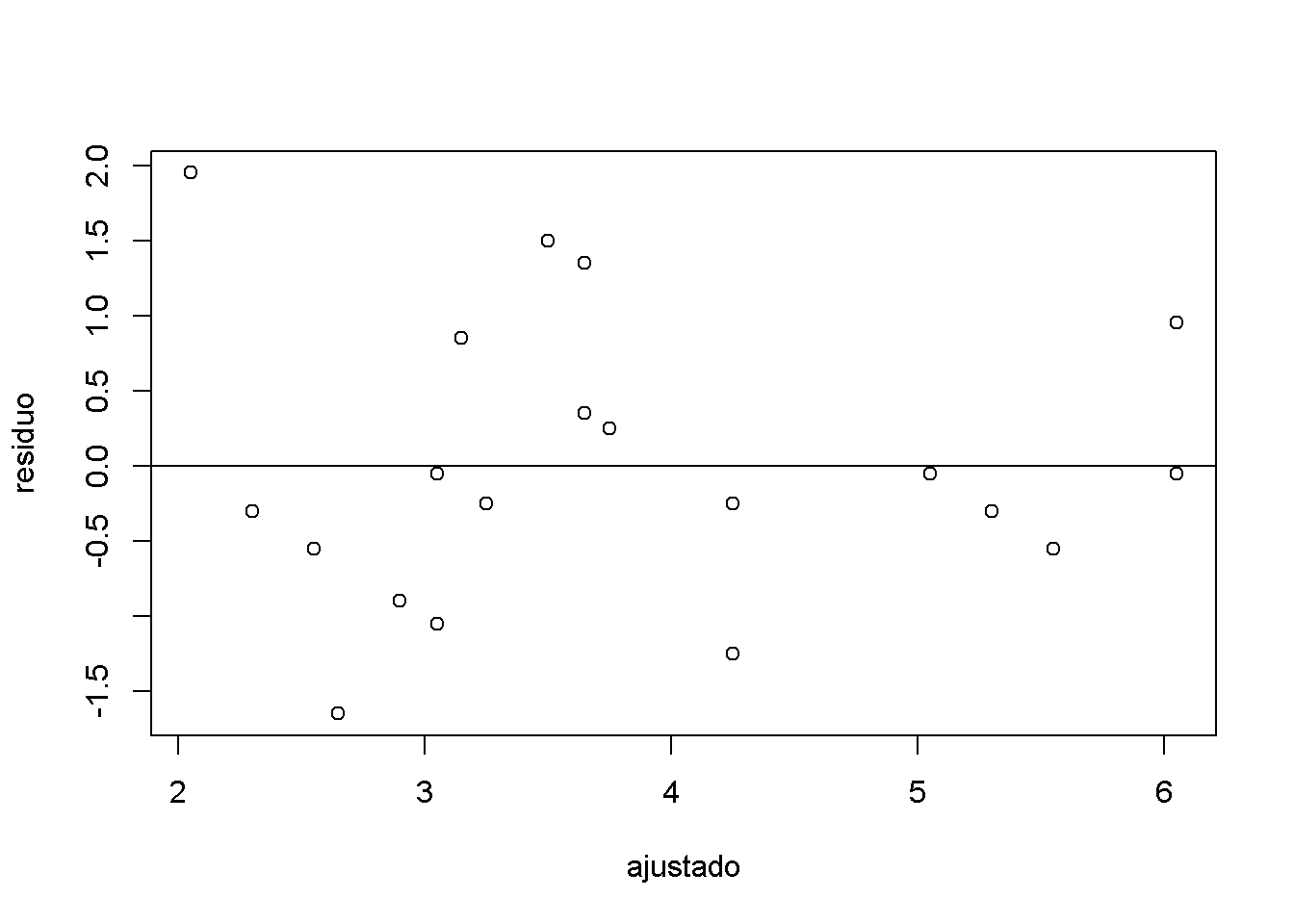

residuo=residuals(anova)
ajustado=fitted(anova)
plot(ajustado,residuo)
abline(h=0)

qqnorm(residuo)
qqline(residuo)

1.6 Exercícios

1. Com o objetivo de avaliar 5 rações (A, B, C, D e E) no ganho de peso animal, um pesquisador instalou um experimento, no delineamento inteiramente casualizado, pois os animais apresentavam características uniformes, utilizando 4 animais (repetições) por tratamento. Os resultados obtidos estão apresentados abaixo.

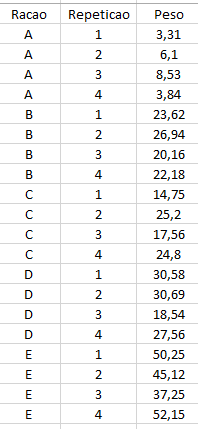
1.1 Foi observada diferença significativa entre as rações avaliadas?

1.2 Por meio do teste de Tukey, qual foi a ração que resultou no maior ganho de peso? De qual não diferiu? Qual foi a ração que resultou no menor ganho de peso? De qual não diferiu?

1.3 Faça a análise descritiva dos resultados obtidos.

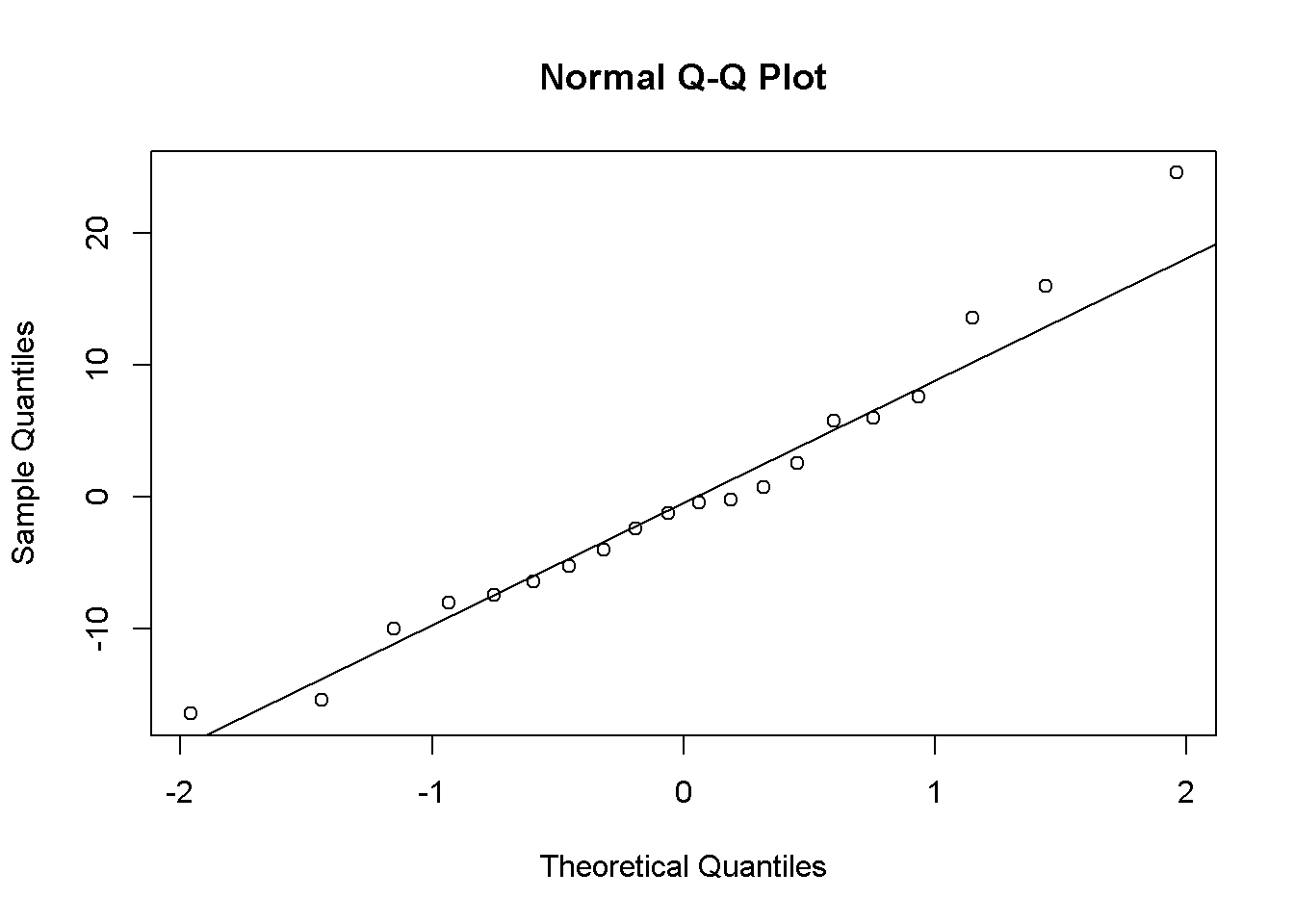
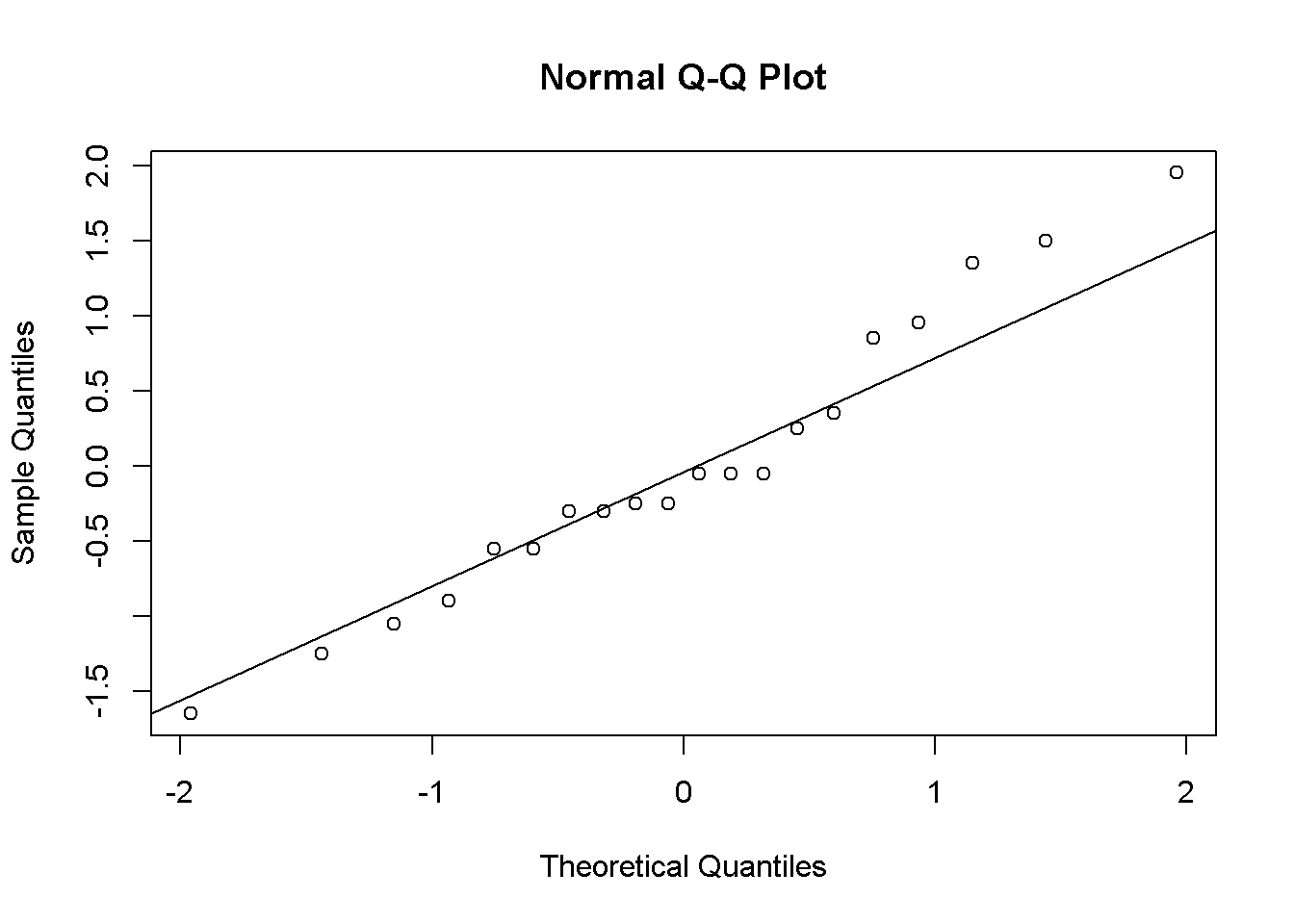
1.4 Faça o gráfico de resíduos da anova.

2. Um experimento foi conduzido no delineamento em blocos casualizados, com cinco blocos, para estudar diferentes métodos de controle de plantas daninhas sobre a produção de grãos de milho, cujo plantio foi realizado em lavoura com diferentes declividades do solo. Os tratamentos e valores de produção de grãos (t/ha) estão apresentados abaixo.

2.1 Foi observada diferença significativa entre os métodos de controle avaliados?

2.2 Por meio do teste de Tukey, qual foi o método de controle que resultou na maior produção? De qual não diferiu? Qual foi o método de controle que resultou na menor produção? De qual não diferiu?

2.3 Faça a análise descritiva dos resultados obtidos.

2.4 Faça o gráfico de resíduos da anova.

3. Objetivando avaliar o rendimento de 4 variedades de macieira (A, B, C e D), instalou-se um experimento sob o delineamento experimental inteiramente casualizado, sendo as parcelas de 8x7m e a lavoura de macieira com 12 anos de idade na época de instalação do experimento. Os dados experimentais a seguir se referem ao peso médio em gramas, de 250 frutos por parcela.

3.1 Foi observada diferença significativa entre as variedades de macieira?

3.2 Por meio do teste de Tukey, qual foi a variedade de macieira que apresentou a maior produção? De qual não diferiu? Qual foi a variedade de macieira que apresentou a menor produção? De qual não diferiu?

3.3 Faça a análise descritiva dos resultados obtidos.

3.4 Faça o gráfico de resíduos da anova.

4. Sejam os resultados do rendimento de grãos (sacos/ha) de um experimento conduzido no delineamento blocos ao acaso com a cultura da soja. Os tratamentos foram 5 (formas) formas de preparo do solo organizados em 5 (cinco) blocos, em função da declividade do terreno.

4.1 Foi observada diferença significativa entre as formas de preparo de solo?

4.2 Por meio do teste de Tukey, qual forma de preparo de solo apresentou o maior rendimento? De qual não diferiu? Qual forma de preparo de solo apresentou o menor rendimento? De qual não diferiu?

4.3 Faça a análise descritiva dos resultados obtidos.

4.4 Faça o gráfico de resíduos da anova